Un fractal es cualquier objeto cuya forma se mantiene independientemente de la escala de observación, es decir, que una parte tiene la misma forma que el todo, sucintamente, invariante por cambio de escala. Por poner un ejemplo, muchos árboles son fractales porque sus pequeñas ramitas recuerdan la forma del conjunto del árbol. También la red dendrítica de los cursos fluviales de montaña se reproduce a variadas escalas, desde el río principal y sus afluentes, hasta los afluentes de estos y, finalmente, los barrancos y arroyos de la cabecera. Los objetos fractales suelen presentar formas muy bellas, estrelladas, ramificadas, repetidas. Los fractales fueron introducidos por el matemático francés Benoît Mandelbrot a finales de los años 60 del siglo XX, y han dado lugar a una nueva geometría, diferente de la euclídea, además de que se relacionan con la famosa Teoría del Caos. Si en la geometría euclídea un punto tiene dimensión 0, una recta 1, un plano 2 y el espacio 3, la geometría fractal permite asignar una dimensión fraccionaria a una línea irregular en el plano, que tendrá una dimensión comprendida entre 1 y 2, tanto más próxima a 2 cuanto más plano ocupe.

El problema de cuánto mide una costa

Uno de los primeros asuntos que atrajo la atención de la teoría de los fractales fue precisamente un problema geográfico: ¿cuánto mide una determinada costa, como, por ejemplo, la costa española? El problema tiene resultados muy diferentes dependiendo de la unidad con que se mida. Así, si se midiera con una regla, rodeando cada pequeña forma de detalle de la costa, el resultado sería elevadísimo, mientras que, si se usara una cinta de 100 m, el resultado sería inferior, dado que las pequeñas sinuosidades de la costa serían consideradas como rectas, y, si se hiciera con segmentos de 100 km sobre un mapa, aún sería menor. En consecuencia, no existe un valor único, lo que sí se puede calcular es su dimensión fractal, que será un número entre 1 y 2, tanto más próximo a 1 cuanto más rectilínea sea, y más próximo a 2, cuanto más recortada e irregularar. Así, en España, la costa gallega, recortada, tiene una dimensión superior a la catalana, bastante rectilínea.

La invariancia de formas por cambio de escala, que define a los fractales en el espacio, puede trasladarse al tiempo, es decir, cabe estudiar si el comportamiento temporal de un fenómeno, como la lluvia, presenta una cierta similitud o autosimilitud en el tiempo. Podría pensarse, como ejemplo ficticio muy simple, si en un lugar con una pauta temporal de 1 hora lluviosa y 3 secas, podría repetirse ese régimen al aumentar la escala, con un día lluvioso y 3 secos, 1 mes lluvioso y 3 secos, 1 año lluvioso y 3 secos, etc. Aun así, mientras en el espacio la identificación de un fractal es visual e intuitiva, con formas a menudo muy llamativas, en el tiempo la invariancia por cambio de escala temporal resulta más difícil de determinar.

Las estaciones meteorológicas automáticas permiten un análisis de la lluvia a una escala temporal fina

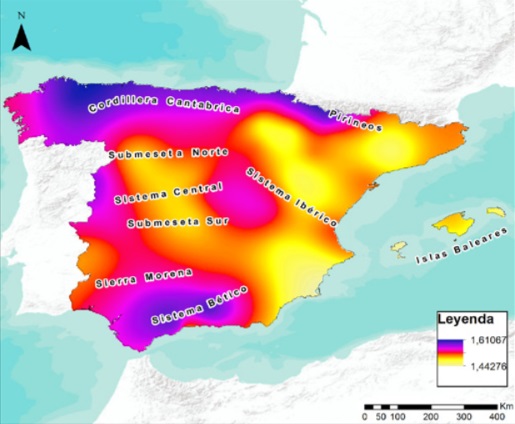
Utilizando una amplia base de datos pluviométricos a resolución 10-minutal de 48 observatorios de la España peninsular y las islas Baleares, pertenecientes a la red automática de la Agencia Estatal de Meteorología (AEMET), se ha calculado la dimensión fractal mediante el método box-counting. Para ello, se parte del período de 10 minutos como el intervalo unitario de base para llevar a cabo el análisis. A continuación se establecen períodos de 10, 20 y 30 minutos, y 1, 2, 3, 4, 6, 8, 12, 24 y 48 horas, y, a partir de los registros pluviométricos a resolución 10-minutal, se contabiliza en cuántos de ellos se registró alguna cantidad de precipitación. Los valores de la dimensión fractal obtenidos están comprendidos entre 1,45 (Ibiza) y 1,60 (Lugo). Los mayores valores de la dimensión fractal se han hallado en el norte, mientras que en la fachada oriental y Baleares y en el valle del Ebro se registran los menores. Por semestres, los valores son más bajos en la mitad cálida del año que en la mitad fría. No es fácil atribuir un significado concreto a los valores de la dimensión fractal obtenidos, por lo que en otros trabajos de los mismos autores se han correlacionado con los valores de varios índices pluviométricos bien conocidos, como con el coeficiente de variación anual, la persistencia de los días lluviosos, etc.

Sin duda, habrá que profundizar más en el conocimiento de la fractalidad temporal de la precipitación, que indaga en la estructura y cadencia temporal de la misma, tan decisiva en diferentes actividades económicas y sociales, desde el agro hasta el transporte, desde la celebración de actos al aire libre hasta el turismo de sol y playa, etc, todos ellos asuntos de los que se ocupa la ciencia geográfica. No está de más recordar que, a menudo, tanta o más importancia tiene el reparto temporal de la lluvia y su ocurrencia en el tiempo, que su cantidad, en especial en países secos.

Para mayor información:

MESEGUER-RUIZ, Óliver, MARTÍN-VIDE, Javier, OLCINA CANTOS, Jorge, SARRICOLEA, Pablo. Análisis y comportamiento espacial de la fractalidad temporal de la precipitación en la España peninsular y Baleares (1997-2010). Boletín de la Asociación de Geógrafos Españoles, 2017, 73, 11:32, DOI: 10.21138/bage.2407.

Javier Martín-Vide es catedrático de Geografía Física y director del Instituto de investigación del Agua de la Universidad de Barcelona.

Los fractales no son solo objetos o figuras con formas bellísimas, sino que su propiedad de invariancia por cambio de escala puede aplicarse también a la ocurrencia temporal de la lluvia.